My broad research interests are in magnetic fields and relativistic astrophysics – with most of my work being at a point where those topics intersect: the magnetic fields of neutron stars. I am a theoretical astrophysicist – whose tools are a pen, paper and computer – rather than a telescope.
Neutron stars are some of the most extreme objects in the Universe, compressing more mass than the Sun (whose radius is 700000 km) into a ball with a radius of roughly 12km. Descending* through their solid crusts, one quickly watches atoms dissolving into a soup of neutrons, protons and electrons. We cannot replicate these conditions in labs here on Earth, and so are left to glean what information we can from observations, and by producing theoretical models of how we think neutron stars work.
*in case you find yourself beside a neutron star, don’t try this yourself – your body’s atoms will suffer the same fate…
One piece of neutron-star physics which makes the theoretician’s life more difficult/interesting is the intense magnetic field harboured by a typical neutron star. This affects pretty much all aspects of the stars’ behaviour and plays a critical role in how we observe them. Briefly, I am interested in what kind of magnetic field structure exists inside and outside a neutron star – and all the ways the field affects the stars’ behaviour. Less briefly, some more details of my interests are listed next.
Equilibrium models of magnetic fields
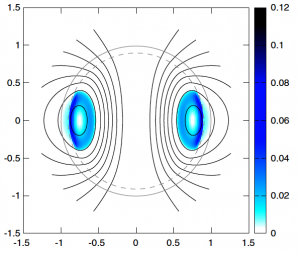
For the most part, we see little evidence of rapid changes in a neutron star’s (internal) magnetic field. This means that one basic requirement of a magnetic-field model is that it is in a steady state. A substantial fraction of the work I have done is on finding equilibrium solutions to systems of equations describing magnetised neutron stars, beginning with simple models of the star as a fluid ball, then incorporating more realistic physics. I have worked on the first models incorporating gradients in the star’s composition, and derived and solved the governing equations for a general poloidal-toroidal magnetic field in a type-II superconductor (since the protons in most of the neutron star’s core are believed to be in this state).
Currently I am trying to understand the magnetic field present in the early life of a neutron star, not long after the supernova in which the star forms. In this formative period the star’s crust is still molten, and strong temperature gradients affect the balance of forces in the star.
Evolution and stability
Just being in equilibrium is only part of the story. To be astrophysically relevant, a magnetic-field model also has to be dynamically stable. This is far harder to show, since there are a vast array of oscillation modes – and just one of those being unstable renders the whole configuration unstable. Providing instability is thus easier than stability. Taking the simplest – but nonetheless widely-used – model for magnetised neutron stars (a barotropic fluid ball), I used numerical time evolutions to perform as comprehensive a survey as I could of equilibrium configurations built in this framework. Unfortunately, all configurations showed at least one unstable mode – suggesting that the incorporation of more realistic neutron-star physics is not only desirable, but essential for constructing a stable field model. One warning though: it’s not that these more realistic models have yet been shown to be stable – but at least noone has yet proven them to be unstable…
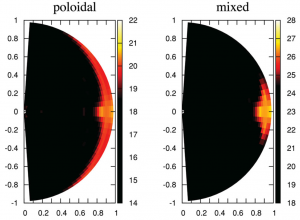
A neutron star’s field also evolves over time, through a number of different processes, as it cools and its rotation rate decreases. For this reason an equilibrium model is never the whole story, and I am beginning to look at this evolution now.
Crustal stresses, coronae, and outbursts
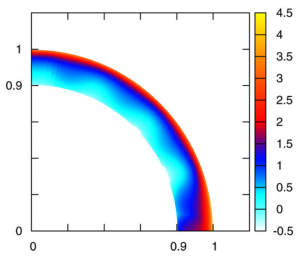
One obvious stabilising agent for a neutron-star magnetic field is its solid crust. This could anchor field lines stably in place, even if the field configuration would have been unstable in the absence of the crust. It also resists the evolution of the magnetic field, but in doing so elastic stresses build in the crustal lattice. Even though the crust is extremely strong, it eventually reaches its yield stress, at which point there could be a sudden change in the internal field. The motion of the crust is an important part of explaining magnetar coronae and outbursts, and I am hoping to gain a quantitative understanding of when and where the crust will yield first.
